leetocode 973

题目描述

973. 最接近原点的 K 个点

给定一个数组 points ，其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点，并且是一个整数 k ，返回离原点 (0,0) 最近的 k 个点。

这里，平面上两点之间的距离是 欧几里德距离（ √(x1 - x2)2 + (y1 - y2)2 ）。

你可以按 任何顺序 返回答案。除了点坐标的顺序之外，答案 确保 是 唯一 的。

示例 1：

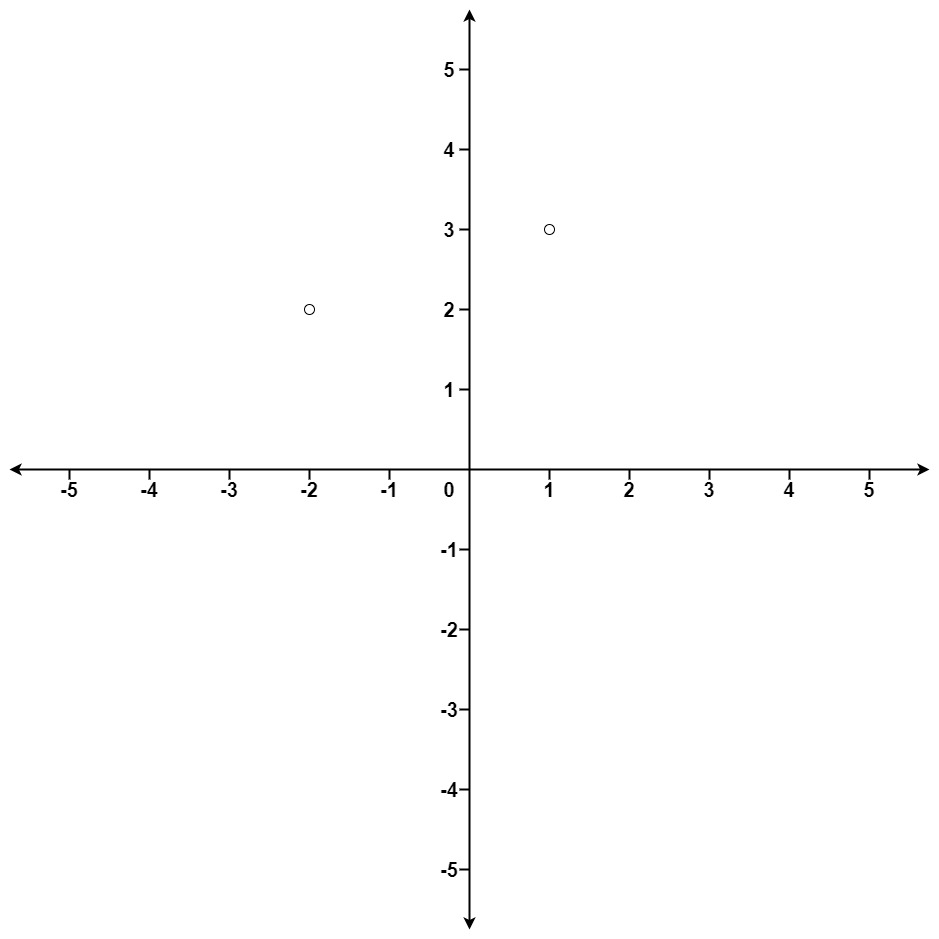
输入：points = [[1,3],[-2,2]], k = 1
输出：[[-2,2]]
解释： 
(1, 3) 和原点之间的距离为 sqrt(10)，
(-2, 2) 和原点之间的距离为 sqrt(8)，
由于 sqrt(8) < sqrt(10)，(-2, 2) 离原点更近。
我们只需要距离原点最近的 K = 1 个点，所以答案就是 [[-2,2]]。

解题思路

1. 直接API排序实现返回
2. 使用优先队列实现（堆）

执行用时：77 ms, 在所有 Java 提交中击败了10.63%的用户

内存消耗：49.8 MB, 在所有 Java 提交中击败了22.19%的用户

通过测试用例：87 / 87

时间 O(n)

空间 O(k)

class Solution {
    private class MyComparator implements Comparator<Integer[]>{
        // 一个大顶堆，peek出的是距离最大的元素
        public int compare(Integer []o1, Integer []o2) {
            return -Double.compare(Math.pow(o1[0], 2) + Math.pow(o1[1], 2), Math.pow(o2[0], 2) + Math.pow(o2[1], 2));
        }
    }
    public int[][] kClosest(int[][] points, int k) {
        MyComparator cmp=new MyComparator();
        PriorityQueue<Integer[]> queue = new PriorityQueue<>(cmp);
        for(int i=0;i<points.length;i++){
            Integer[] tmp=new Integer[]{points[i][0],points[i][1]};
            if(i<k){
                queue.offer(tmp);
            }
            // 如果当前元素小于queue中距离最大的元素则更新
            else if(cmp.compare(tmp,queue.peek())>0){
                queue.poll();
                queue.offer(tmp);
            }
        }
        int [][]ans=new int[k][2];
        for(int i=0;i<k;i++){
            Integer[]tmp=queue.poll();
            ans[i][0]=tmp[0];
            ans[i][1]=tmp[1];
        }
        return ans;
    }
}